ÁLGEBRA I

MONOMIOS Y POLINOMIOS.

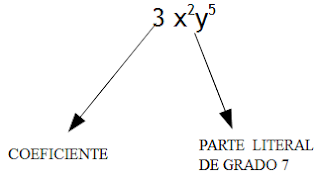
Llamaremos monomio a cualqier expresión algebraica de la forma

Se entiende que se trata de un producto de tres factores, un número conocido, que es el coeficiente 3 y dos potencias de números desconocidos que se representan por letras, x e y. En el lenguaje matemático usamos las letras para representar números desconocidos o también variables. En el ejemplo, el coeficiente es el número entero 3 y lo que llamamos parte literal está formado por los números indeterminados x²y⁵ , es decir el producto del cuadrado del número x y la quinta potencia de y. Los exponentes de las potencias nos dan el grado del monomio que se obtiene sumando los exponentes de las indeterminadas x e y, es decir, en este ejemplo el grado es 2 + 5 = 7.

INTERÉS BANCARIO.

LA FÓRMULA DEL INTERÉS SIMPLE

En esta nota abordaremos el problema del interés bancario. Como todo el mundo sabe, el interés consiste en el precio del dinero, cuando se presta dinero este préstamo se hace a cambio de una retribución: el interés. El negocio de un banco consiste en prestar dinero, pero para ello debe tener depósitos de sus clientes, los cuales obtienen una retribución por adquirir los productos financieros ofrecidos por los bancos. Esta retribución del dinero prestado es el interés. El interés de un préstamo puede ser de dos clases: simple o compuesto. Veremos aquí en qué consiste el interés simple, es muy fácil.

PROPORCIONALIDAD COMPUESTA II

Ejercicios propuestos de Proporcionalidad Compuesta.

1. 15 obreros trabajando 6 horas diarias, tardan 30 días en realizar un trabajo. ¿Cuántos días tardarán en hacer el mismo trabajo 10 obreros, empleando 8 horas diarias?
2. En una fábrica 5 máquinas llenan 7.200 envases en 6 horas. ¿Cuántos envases llenarán 7 máquinas en 8 horas?

PROPORCIONALIDAD COMPUESTA I

En muchos problemas intervienen varias magnitudes a considerar, no solamente dos como ocurre en los problemas de proporcionalidad simple. A estos problemas cuando hay múltiples relaciones de proporcionalidad los llamamos problemas de proporcionalidad compuesta. En estas notas veremos de qué se trata.

Supongamos que tenemos tres magnitudes que llamaremos A, B y C. La relación de A con B es de proporcionalidad directa y por otro lado A y C son inversamente proporcionales. Hemos tomado medidas a, b, c y a', a'', b', c' de las magnitudes A, B y C como se puede ver en la tabla siguiente.

REPARTOS PROPORCIONALES

A continuación vamos a estudiar los problemas de reparto proporcional que pueden ser bien de proporcionalidad directa o bien de proporcionalidad inversa.

Un problema típico de reparto proporcional directo es el de la regla de la compañía donde cabe repartir beneficios entre los socios de la empresa de manera directamente proporcional a la participación de cada uno en el capital de la misma.

En una relación de proporcionalidad directa, donde los números a, b, c son directamente proporcionales a los números a', b', c' sabemos que se cumple la proporción:

Más sobre cuestiones de Proporcionalidad

Hola a todos,

Abundando más en el tema de la proporcionalidad os traigo hoy un enlace que puede ser interesante, pincha y haz clic en este enlace.

proporcionalidad

EJERCICIOS DE PROPORCIONALIDAD Y PORCENTAJES

1.- Indica si hay proporcionalidad directa, inversa o si no hay ninguna proporcionalidad:

a) Cantidad de personas que viajan en un autobús y dinero recaudado.

b) Cantidad de refrescos que caben en una caja y diámetro de las botellas.

c) Número de litros que escapan por segundo en el desagüe de una piscina y diámetro del desagüe.

d) Velocidad media de un ciclista y distancia recorrida.

e) Número de vueltas que da una rueda para recorrer una distancia y diámetro de la rueda.

f) Número de comensales para zamparse una tarta y cantidad que corresponde a cada uno.

g) Tiempo que tarda un balón en caer al suelo y altura desde la que se lanza.

h) Número de horas que está encendida una bombilla y gasto que ocasiona.

i) Número de peldaños de una escalera móvil de altura fija y separación entre ellos.

j) Número de peldaños de una escalera de altura fija y anchura de ellos.

k) Numero de goles marcados por un equipo y partidos ganados.

PROPORCIONALIDAD Y PORCENTAJES

Razón entre dos cantidades.

Por razón entre dos números fijos o dos variables se entiende el cociente entre ambas. Por ejemplo si de 40 alumnos que se presentan al examen para el permiso de conducir aprueban 30, entonces la razón de los aprobados es de 30 sobre 40, 30/40 o 3/4 o 3 de cada 4, o de 0,75 por 1 o del 75%. Una razón o ratio también suele expresarse como un tanto por ciento. Para calcular una razón como porcentanje, hacemos

Entonces diremos que aprueban el 75% de los aspirantes que se presentan al examen del permiso de conducir.

Proporción.

Por proporción entenderemos cualquier igualdad de razones, es decir una proporción es

Los números a y d reciben el nombre de extremos de la proporción. Los números b y c reciben el nombre de medios de la proporción.

MÁS PROBLEMAS SOBRE FRACCIONES

Como he prometido en las clases, voy a publicar aquí más ejercicios o problemas que se resuelven operando con fracciones para que podáis practicar en los ratos libres. Al final dejo las soluciones a los ejercicios simplemente indicadas. Comprobar si tenéis los ejercicios correctamente resueltos y preguntar cualquier duda. Un cordial saludo, que se os den bien los ejercicios.

1. En una ciudad de 24.000 habitantes, los 4/15 saben hablar perfectamente la lengua inglesa. ¿Cuántas personas de esta ciudad hablan inglés correctamente?
2. En unas oposiciones se presentan 3.600 aspirantes, pero tan solo reciben la calificación de APTO unos 45 aspirantes. ¿Cuál es la ratio de personas "APTAS" en esta oposición?
3. ¿Cuántas botellas de 3/4 de litro se pueden llenar con 180 litros de aceite?
   

RESOLUCIÓN DE PROBLEMAS MEDIANTE FRACCIONES

TEMA 1. NÚMEROS RACIONALES. FRACCIONES Y DECIMALES.

RESOLUCIÓN DE PROBLEMAS.

En estos apuntes primero pondré unos ejemplos de resolución de problemas mediante el uso de fracciones para a continuación dejar propuestos varios ejercicios que espero sean de provecho para el alumno.

EJERCICIOS RESUELTOS.

Ejercicio resuelto 1.

En hotel hay 540 habitaciones de las cuales 120 son individuales y el resto son habitaciones dobles. Expresa mediante una fracción la proporción de habitaciones simples y dobles que tiene este hotel.

Solución.

La proporción de habitaciones simples esta expresada por la fracción 

Hay que recordar que las fracciones deben simplificarse.

La proporción de habitaciones dobles será entonces 1 – 2/9 = 9/9 - 2/9 = 7/9

TEMA 1. NÚMEROS RACIONALES

Los siguientes ejercicios representan una perspectiva general de lo que constituye la primera unidad temática del presente curso. Toma lápiz y papel, realiza las actividades propuestas. Más adelante publicaré las soluciones a los ejercicios de esta hoja. ¡Manos a la obra y que se os dé bien!

1. Realiza las siguientes operaciones simplificando los resultados todo lo que puedas, esto es hasta una fracción irreducible.