En muchos problemas intervienen varias magnitudes a considerar, no solamente dos como ocurre en los problemas de proporcionalidad simple. A estos problemas cuando hay múltiples relaciones de proporcionalidad los llamamos problemas de proporcionalidad compuesta. En estas notas veremos de qué se trata.
Supongamos que tenemos tres magnitudes que llamaremos A, B y C. La relación de A con B es de proporcionalidad directa y por otro lado A y C son inversamente proporcionales. Hemos tomado medidas a, b, c y a', a'', b', c' de las magnitudes A, B y C como se puede ver en la tabla siguiente.
A | B | C |
a | b | c |
a'' | b' | c |
a' | b' | c' |
Manteniendo C constante (la cantidad c no varía) , A y B son directamente proporcionales, luego
Por otro lado, con B constante (la cantidad b' no cambia) tendremos que A es inversamente proporcional a C y por tanto
Y multiplicando ambas expresiones anteriores obtenemos una relación de proporcionalidad compuesta entre las tres magnitudes A, B y C. A saber:
En resumen, como A es directamente proporcional a B e inversamente proporcional a C se verifica la relación de proporcionalidad compuesta
Y si A es directamente proporcional a B y también a C, entonces
Por último, si A es inversamente proporcional a B y también a C entonces tendremos la proporción compuesta
Veremos todo esto más claro con algunos ejemplos de ejercicios resueltos
Ejemplo 1.
Tres personas pagan en un hotel 810 euros por 10 noches de estancia. ¿Cuánto tendrían que pagar 10 personas por 15 noches?
Solución:
Tenemos que plantear la siguiente tabla de datos:
Precio | Nº Noches | Nº de personas |
810 | 10 | 3 |
x | 15 | 10 |
El precio es directamente proporcional al número de noches y al número de personas, por tanto tenemos la regla de tres compuesta:
Lo que nos da que el precio total debe ser de 4.050 €, en efecto:
Este método de resolución es la regla de tres compuesta. Otro método para resolver el problema consiste en la reducción a la unidad y sería lo siguiente:
Precio | Noches | Nº de personas |
810 | 10 | 3 |
(810:10):3 = 27 | 1 | 1 |
x | 15 | 10 |
Primero averiguamos lo que abona una persona por una noche, a saber 810/(10·3) = 27 € por persona y noche. Luego 10 personas tendrán que pagar por 15 noches la cantidad x= 10·15· ·27 = 4.050 € .
Ejemplo 2.
Cinco obreros son capaces de arreglar 6 km de carretera en 3 días. ¿Cuántos obreros más serían necesarios para arreglar 12 km de carretera en 5 días?
| Nº de obreros | Km de carretera | Tiempo (días) |
| 5 | 6 | 3 |
| x | 12 | 5 |
El número de obreros es directamente proporcional al trabajo realizado e inversamente proporcional al tiempo empleado en hacerlo. La regla de tres compuesta es entonces
de donde tenemos que
Por tanto la solución consiste en que hay que contratar un obrero más.
Ejemplo 3.
Cinco obreros de una fábrica, trabajando en jornadas de 8 horas al día, consiguen terminar un trabajo en 10 días. ¿Cuántas horas díarias tendrían que emplear 10 obreros para realizar el mismo trabajo en 4 días?
Jornada (horas/día) | Nº obreros | Tiempo (días) |
8 | 5 | 10 |
x | 10 | 4 |
La jornada laboral debe ser inversamente proporcional al número de obreros (manteniendo el trabajo constante) y también inversamente proporcional al número de días. Aplicando la regla de tres compuesta tendremos que
de donde obtenemos la solución
Solución: La jornada laboral tendría que prolongarse dos horas más, sería de 10 horas diarias.
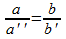

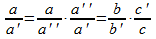









No hay comentarios:
Publicar un comentario