MONOMIOS Y POLINOMIOS.
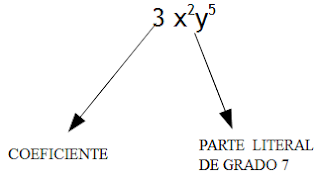
Llamaremos monomio a cualqier expresión algebraica de la forma
Se entiende que se trata de un producto de tres factores, un número conocido, que es el coeficiente 3 y dos potencias de números desconocidos que se representan por letras, x e y. En el lenguaje matemático usamos las letras para representar números desconocidos o también variables. En el ejemplo, el coeficiente es el número entero 3 y lo que llamamos parte literal está formado por los números indeterminados x2y5 , es decir el producto del cuadrado del número x y la quinta potencia de y. Los exponentes de las potencias nos dan el grado del monomio que se obtiene sumando los exponentes de las indeterminadas x e y, es decir, en este ejemplo el grado es 2 + 5 = 7.
En un monomio el coeficiente puede ser cualquier clase de número, entero, racional o irracional. Sin embargo, los exponenentes de las indeterminadas x, y, z, etc... tienen que ser números enteros positivos. Por ejemplo, no son monomios las siguientes expresiones
Tenemos muchos ejemplos de monomios en muchas fórmulas matemáticas o leyes de Física. Por ejemplo:
Área de un triángulo:
Área de un triángulo:
Volumen de un prisma de altura h y base cuadrada de lado x: V = x2h
Ley de Ohm: V=I·R
donde V es la tensión eléctrica o diferencia de potencial eléctrico, I es la intensidad de la corriente eléctrica y la constante R es la resistencia del circuito eléctrico.
Espacio recorrido en un movimiento rectilíneo uniforme a velocidad constante v en un tiempo t: s=v·t
Diremos que dos monomios son semejantes si tienen idéntica parte literal, por ejemplo son semejantes 5xy3 y -2xy3 , la única diferencia está en el coeficiente.
Los monomios semejantes los podemos sumar aplicando la propiedad distributiva. Por ejemplo:
aquí el factor común de ambos sumandos es xy, es decir la parte literal.
También podemos multiplicar cualquier par de monomios, por ejemplo:
Sin embargo para poder dividir monomios, los exponentes del dividendo tienen que ser mayores que los exponentes del divisor. Por ejemplo:
En otro caso, lo que tendremos será una fracción algebraíca, por ejemplo:
Valor numérico asociado a un monomio.
Cuando le asignamos un valor numérico a cada una de las variables que intervienen en un monomio, por ejemplo x=5 y=2 entonces al multiplicar obtenemos un valor numérico para el monomio
Expresiones algebraicas.
En muchos problemas se plantean relaciones entre variables, incógnitas o cualquier tipo de datos conocidos o desconocidos y estas relaciones deben traducirse en lenguaje matemático para poder operar con ellas y plantear ecuaciones que resuelvan el problema.
Por ejemplo, la expresión el doble de un número menos su séptima parte se traduce en la siguiente expresión simbólica:
La expresión el cuadrado de un número menos su mitad se traduce en
POLINOMIOS.
Por polinomio entenderemos cualquier suma de monomios que no son semejantes. Por ejemplo:
Los monomios de un polinomio los podemos ordenar por su grado, el mayor de todos ellos es el grado del polinomio. Por ejemplo el polinomio
está ordenado y tiene grado 3.
En todo lo que sigue vamos a considerar tan solo polinomios de una indeterminada, aunque los polinomios pueden ser de varias indeterminadas x, y, z, etc.
Dependiendo del número de monomios que tenga el polinomio podemos llamarlo binomio (es decir, con dos monomios), trinomio (con tres monomios), etc. Los polinomios los nombraremos con letra mayúscula y entre paréntesis la indeterminada o variable, por ejemplo A(x), B(x), etc.
Polinomio completo es el que posee monomios de todos los grados inferiores a su grado. Por ejemplo,
es completo, aunque no está escrito de manera ordenada.
En cambio,
es un polinomio de grado 4 pero no es completo, aunque si está escrito de manera ordenada.
Valor numérico de un polinomio.
Un polinomio no es más que una receta o fórmula para hacer operaciones aritméticas. Por ejemplo, tomemos el polinomio de grado 3.
Entonces, al dar un valor numérico a la variable x como por ejemplo x= - 2 entonces calculamos según las operaciones indicadas en el polinomio y obtenemos un número, a saber
OPERACIONES CON POLINOMIOS
Suma de polinomios.
Se suman los polinomios término a término. Por ejemplo:
Resta de polinomios.
El opuesto de un polinomio P(x) es el polinomio -P(x). Por ejemplo, el opuesto de
es el polinomio
La resta de dos polinomios consiste en sumar uno con el opuesto del otro. Por ejemplo, sean
Producto de polinomios.
Multiplicar un polinomio por un monomio es fácil, multiplicamos cada monomio del polinomio por el monomio multiplicador. Por ejemplo,
Para multiplicar polinomios tenemos que aplicar la propiedad distributiva del producto respecto de la suma, y multiplicar todos y cada uno de los monomios del primer polinomio por todos y cada uno de los monomios del segundo polinomio. Por ejemplo:
También podemos multiplicar polinomios del siguiente modo, igual que en el algoritmo de la multiplicación con números.
ALGORITMO DE LA DIVISIÓN DE POLINOMIOS.
Dados dos polinomios P(x) y Q(x) con grado P = m mayor que el grado Q =n entonces podemos encontrar un único polinomio C(x) de grado m – n y un único polinomio R(x) con grado estrictamente inferior al grado de Q, grado R < grado Q. De modo que se cumple la relación
En el siguiente vídeo podemos ver como se efectúa la división paso a paso.
En el siguiente vídeo podemos ver como se efectúa la división paso a paso.
No hay comentarios:
Publicar un comentario