LAS IDENTIDADES NOTABLES.
Una identidad es una relación de igualdad entre dos expresiones algebraicas que se verifica de manera independiente de los valores numéricos que puedan adquirir todas las variables implicadas en dichas expresiones.
Por ejemplo:
o por ejemplo
son identidades algebraicas.
En lo que sigue vamos a estudiar tres identidades que son claves en las operaciones algebraicas más comunes porque permiten agilizar los cálculos con expresiones algebraicas, se suelen usar tanto en resolución de ecuaciones como a la hora de descomponer en factores un polinomio.
Primera identidad notable: Cuadrado de una suma de dos números.
Para cualquier par de números a y b se cumple la identidad
Es decir el cuadrado de la suma es igual a la suma de los cuadrados más el doble del primero por el segundo términos de la suma.
Esta identidad se puede apreciar bien en el siguiente esquema gráfico:
Operando algebraicamente, aplicando la propiedad distributiva del producto y la propiedad conmutativa obtenemos que
Segunda identidad notable: Cuadrado de una diferencia de dos números.
La segunda de estas identidades afirma lo siguiente: Para cualquier par de números a y b el cuadrado de su diferencia es igual a la suma de los cuadrados de ambos términos menos el doble del primero por el segundo, esto es en lenguaje algebraico
Visualmente la identidad algebraica se puede ver en la siguiente figura
Las áreas de los rectángulos de color azul y amarillo son iguales entre sí y la suma con el cuadrado de lado a – b de color magenta nos da el resultado esperado.
Es decir, lo que se observa en el gráfico es la igualdad
Operando algebraicamente tendremos
Expresión que se deduce de la propiedad distributiva y conmutativa del producto.
Tercera identidad notable. Producto de dos términos conjugados.
La tercera de las identidades notables establece que la suma de dos números a y b multiplicada por su diferencia equivale a la diferencia de los cuadrados de a y b. Es decir:
Se suele decir que la expresión a – b es conjugada de a + b. Esta identidad se puede apreciar con el siguiente gráfico
Las áreas de los rectángulos de color amarillo son iguales entre sí, a saber (a-b)b. Algebraicamente, aplicando la propiedad distributiva y conmutativa de la multiplicación o producto tendremos que
EJEMPLOS.
- Descomponer en factores los siguientes polinomios
SOLUCIÓN.a) Primero se saca factor común, entonces quedaría
b) Igual que antes, primero sacamos factor común, quedando
c) Este trinomio cuadrático es un cuadrado perfecto, en efecto:
d) Sacamos primero un factor común y tenemos:

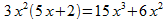















muy bien explicado!!
ResponderEliminarGracias por tu comentario. No he recibido muchos. Te animo a seguir leyendo, hay muchos blogs de matemáticas.
ResponderEliminarEstaá genial!! Muchas gracias por la explicación :)
ResponderEliminar