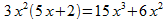Tema 2. Potencias y raíces. Notación científica. Números irracionales.

En la entrada de hoy publico los apuntes del tema 2 dedicado fundamentalmente a las potencias y raíces de números reales. Los números reales son aquellos del conjunto formado por todos los números racionales y los números irracionales. Los números irracionales son aquellos números que no se pueden representar por una fracción o cociente entre números enteros, por ejemplo suelen aparecer cuando se toman las raíces de cualquier número.

POTENCIAS Y RAÍCES

Hola de nuevo,

Lo que sigue es una hoja de ejercicios, a modo de resumen, de la unidad temática sobre potencias y radicales. No son ejercicios rebuscados o difíciles, espero que sean de utilidad para el estudio y la preparación de los exámenes.

Saludos,

RESUMEN DE EJERCICIOS DE LOS TEMAS 0 Y 1

A continuación incluyo un pequeño resumen de ejercicios con números enteros y fracciones. Estos ejercicios  los resolveremos en clase, de todos modos aquí también publicaré las soluciones.

Saludos,

SOLUCIONES A LOS EJERCICIOS

Hoy publico las soluciones a los ejercicios sobre cálculo con fracciones que corresponde a la entrada del día 6 de Octubre: "Ejercicios de cálculo con fracciones". Ante cualquier duda con algún ejercicio no dudéis en consultarme.

Saludos,

EJERCICIOS CON FRACCIONES

En la entrada de hoy publico otra lista de 22 ejercicios de cálculo con fracciones, he mezclado ejercicios de dificultad variada, unos fáciles y otros algo más difíciles. Si tenéis cualquier duda poneos en contacto conmigo para resolverla. Más adelante publicaré las soluciones. Tengo que insistir en que realicéis las operaciones paso a paso y simplificando las fracciones sobre la marcha antes de hacer las cuentas, esto os ayudará a que éstas sean más sencillas, esto es un consejo importante, de otro modo podéis cometer muchos errores o hacer más difíciles las operaciones.

Saludos.

SOLUCIONES A LOS EJERCICIOS

Hola, en esta entrada del blog voy a publicar las soluciones a los ejercicios propuestos en la primera hoja de operaciones con números enteros y fracciones.
Sin más comentarios, aquí están estas soluciones:

TEMA 1. NÚMEROS RACIONALES.

Este tema trata sobre los números racionales. Empezamos con las fracciones, vemos el concepto de equivalencia (dos fracciones equivalentes representan la misma razón) para definir el número racional como una clase de fracciones equivalentes entre sí. A continuación se trata sobre las operaciones con números racionales o fracciones, los números decimales periódicos y la fracción generatriz. Hay ejercicios resueltos y ejercicios propuestos para realizar.

NÚMEROS ENTEROS Y DIVISIBILIDAD. M.C.D. y m.c.m.

Bien, aquí os dejo el tema de inicio del curso. Un repaso sobre el sistema de los números enteros.

EJERCICIOS DE ARITMÉTICA BÁSICA

A continuación publico unos ejercicios para resolver en casa, más adelante publicaré las soluciones.
Son los siguientes:

RECUPERACIÓN EN LA CONVOCATORIA DE SEPTIEMBRE

Cosas que hay que estudiar para pasar el examen de septiembre:

1. Operaciones con fracciones. Números decimales periódicos. Fracción generatriz. Operaciones combinadas con fracciones y números decimales.
2. Potencias y raíces. Operaciones con potencias. Operaciones con radicales.
3. Operaciones con porcentajes. Aumentos y disminuciones porcentuales. Tasa de variación.
4. Proporcionalidad. Regla de tres simple. Regla de tres compuesta. Interés simple. Repartos directamente proporcionales. Repartos inversamente proporcionales.
5. Expresiones algebraicas. Valor numérico de una expresión algebraica. Operaciones con polinomios: suma, resta, producto y división. Operaciones combinadas con polinomios. Identidades notables. Regla de Ruffini. Teorema del resto y teorema del factor. Factorización de polinomios.
6. Ecuaciones de primer grado. Ecuaciones de segundo grado. Sistemas de ecuaciones de primer grado. Métodos de resolución: sustitución, igualación y reducción. Resolución gráfica de un sistema de ecuaciones de primer grado. Resolución de problemas mediante ecuaciones.
7. Geometría. Teorema de Thales. Teorema de Pitágoras. Teoremas de la altura y del cateto. Triángulos, cuadriláteros, polígonos, polígonos regulares y círculos. Perímetros y áreas de figuras del plano.

TEOREMA DE THALES.

TEOREMA DE THALES

Teorema 1.

Sean las rectas del plano r, s con intersección en el punto O y sean las rectas paralelas AB y A'B' tal y como se aprecian en la figura (1). Entonces se cumple la proporción

figura 1

RADICALES

Definición: Un número b es raíz de índice n, o raíz n-ésima, del número a si resulta que bⁿ = a. Más concretamente, escribimos simbólicamente, 

siendo a (el número bajo el signo de la raíz ) el radicando.

RESOLUCIÓN DE ECUACIONES I

RESOLUCIÓN DE ECUACIONES.

En este tema nos vamos a referir a la resolución de ecuaciones algebraicas. Una ecuación algebraica es una relación de igualdad entre dos expresiones algebraicas denominadas miembros de la ecuación, primer miembro (situado a la izquierda del signo =) y segundo miembro (situado a la derecha del signo =). Por ejemplo:

PROBLEMAS DE ECUACIONES DE PRIMER GRADO

Aquí van los enunciados de una serie de problemas, más adelante publicaré las soluciones correctas.

1. Si hace 8 minutos faltaban 9/5 del tiempo que ahora falta para llegar a las 10 horas de la mañana, ¿qué hora es?

2. Un padre tiene 27 años más que su hijo y hace 8 años la edad del padre doblaba la del hijo. ¿Cuáles son las edades de ambos?

3. Marta pagó por un pantalón 35€, con un descuento aplicado del 12%. ¿Cuál era el precio del pantalón antes de la rebaja?

4. Un anticuario ha comprado un mueble por 250€. Manda reparar el mueble y lo vende por 620€. Este anticuario obtiene un beneficio que se cifra en los 2/15 del dinero invertido. ¿A cuánto ascendía el coste de la reparación?

DESCOMPOSICIÓN DE UN POLINOMIO EN FACTORES

TEOREMA DEL RESTO.

Cuando dividimos un polinomio P(x) por el binomio x – a obtenemos un cociente C(x) y un resto R , que es un valor numérico. De manera que

A la vista de esta expresión es fácil ver que cuando x = a, tendremos que el valor numérico del polinomio es P(a)=R. Por ejemplo:

En la división

REGLA DE RUFFINI

La regla de Ruffini consiste en un método para dividir cualquier polinomio P(x) por un binomio de la forma x – a. Veamos como funciona con el siguiente ejemplo:

IDENTIDADES NOTABLES

LAS IDENTIDADES NOTABLES.

Una identidad es una relación de igualdad entre dos expresiones algebraicas que se verifica de manera independiente de los valores numéricos que puedan adquirir todas las variables implicadas en dichas expresiones.

Por ejemplo:

o por ejemplo

son identidades algebraicas.

En lo que sigue vamos a estudiar tres identidades que son claves en las operaciones algebraicas más comunes porque permiten agilizar los cálculos con expresiones algebraicas, se suelen usar tanto en resolución de ecuaciones como a la hora de descomponer en factores un polinomio.

Primera identidad notable: Cuadrado de una suma de dos números.

Para cualquier par de números a y b se cumple la identidad

Es decir el cuadrado de la suma es igual a la suma de los cuadrados más el doble del primero por el segundo términos de la suma.