Un
poco de geometría...
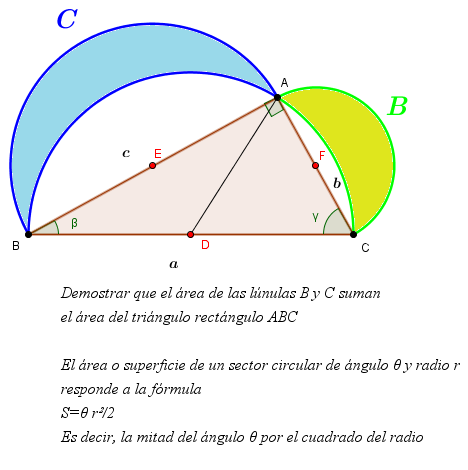
En el triángulo
rectángulo ABC se han
dibujado en los lados dos especies de formas de luna, los límites o
lados de la figura C son:
la semicircunferencia AB
con centro en el punto medio E, y el arco de circunferencia AB
con centro en el punto medio del lado BC, el punto D. Para la figura
B, lo mismo.
Nota: Aquí hay que reseñar que los ángulos los estoy midiendo en radianes, lo he supuesto así para mi mayor comodidad. No es difícil el concepto de radián pero para los novatos es desconocido. Baste decir que pi radianes equivalen a 180º sexagesimales.
Por un argumento de semejanza, el área del triángulo ABD es justo la mitad de la del triángulo rectángulo ABC. Del mismo modo, también el área del triángulo
ADC es, la misma que la mitad del triángulo ABC. Entonces
El área de la luna C es entonces
Nota: revisar el tópico sobre
los ángulos en una circunferencia.
Y para la luna B, pues análogamente
Sumando
Los ángulos B y C son complementarios,
suman uno recto, obviamente.
Esto es todo amigos.




Me parecen geniales los problemas
ResponderEliminarGracias Elia,
ResponderEliminarPor tus comentarios, acabo de leerlos. No me había metido en el blog hasta ahora. Lo tengo un poco descuidado. Lleva trabajo sostener este tipo de cosas y muchas veces me aburro o no encuentro interés o inspiración. Hasta pronto.