Cuando
en enseñanza secundaria se estudian los elementos de los triángulos
como son sus líneas notables (alturas, medianas y bisectrices)
normalmente se omiten muchas cosas, como por ejemplo una sencilla ley
que cumplen las bisectrices y que aquí he llamado Teorema de la
bisectriz. Es un muy buen ejemplo de demostración, de
razonamiento lógico-matemático con el que se puede instruir
a los alumnos de tercero o cuarto de ESO en cultivar la competencia matemática ( para aquellos que manifiesten algún tipo
de interés, por supuesto).
El
enunciado del teorema vendría a ser el siguiente:
En
todo triángulo ABC,
si trazamos la bisectriz del ángulo A, ésta secciona
a su lado opuesto, a, en dos segmentos m, n,
proporcionales
a los lados del ángulo, b y c.
La
demostración es bien sencilla.
Primero,
hay que tener en cuenta la definción de bisectriz:
La
bisectriz es el lugar geométrico de los puntos equidistantes de los
lados
Después
razonamos sobre los triángulos en que se descompone la figura.
Si
(ABD) es
el área del triángulo ABD.
Entonces,
y también
luego,
Análogamente,
sobre el triángulo ADC
por
tanto,
Q.E.D.


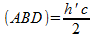
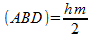

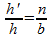

No hay comentarios:
Publicar un comentario